Valores extremos

Podemos encontrar más rápidamente los valores extremos de una función $f (x, y)$ con la ayuda de las primeras derivadas parciales
Un valor extremo existe en una de 3 situaciones:
1. Un punto frontera del dominio
2. Un punto interior donde las primeras derivadas parciales se anulan $(f_{x} = f_{y} = 0)$
  - ! No siempre indica valor extremo, podría ser punto de silla
3. Al menos una de las derivadas parciales no existe
Buscaremos puntos donde la superficie $z = f (x, y)$ tenga un plano tangente horizontal
Máximo local: $f (a, b)$ es un valor máximo local de $f$ si $f (a, b) \geq f (x, y) \forall (x, y)$ del dominio en un disco abierto con centro en $(a, b)$
Mínimo local: Si $f (a, b) \leq f (x, y) \forall (x, y)$ del dominio en un disco abierto con centro en $(a, b)$

Teorema 10: Criterio de la primera derivada para extremos locales

Si $f (x, y)$ tiene un valor máx./min. local en un punto interior $(a, b)$ de su dominio
Si las primeras derivadas parciales existen allí
Entonces $f_{x} (a, b) = f_{y} (a, b) = 0$

Punto crítico de $f$ : Es un punto interior del dominio de la función donde todas las derivadas se anulan ( $f_{x} = f_{y} = 0$ ), o alguna de estas no existe
Punto de silla: Es un punto crítico $(a, b)$ donde, para todo disco abierto con ese centro, existen puntos del dominio donde la función toma valores mayores que $f (a, b)$ y en otros puntos toma valores menores
- Análogo al punto de inflexión de una función de una variable
Hessiano/Discriminante de $f$ : Es el determinante $H (x, y) = | \begin{matrix} f_{x x} & f_{y x} \\ f_{x y} & f_{y y} \end{matrix} | = f_{x x} f_{y y} - f_{x y}^{2}$
- Recordamos que $f_{x y} = f_{y x}$
- Si es positivo ~
- Si es negativo ~

Teorema 11: Criterio de la segunda derivada

Máximo local si $[\begin{matrix} H (a, b) > 0 \\ f_{x x} < 0 \end{matrix}]$
Mínimo local si $[\begin{matrix} H (a, b) > 0 \\ f_{x x} > 0 \end{matrix}]$
Punto silla si $H (a, b) < 0$
Si $H (a, b) = 0$ el criterio es no concluyente

Multiplicadores de Lagrange

Es un método utilizado para encontrar valores extremos de una función con el dominio restringido a un subconjunto del plano (como un disco o una región triangular, etc).
Lo usamos cuando el dominio está restringido por una regla

& Si queremos buscar el punto de un plano más cercano al origen, se plantea buscar la función distancia que tenga un valor mínimo, pero que tome como parámetro sólo los puntos pertenecientes al plano
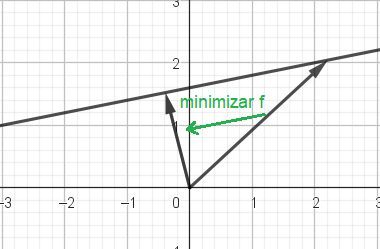
- & La función distancia $d (x, y, z) = \sqrt{x^{2} + y^{2} + z^{2}}$ tiene un mínimo absoluto en $O (0, 0, 0)$ , pero $O$ no pertenece al plano de la restricción!

Máximos y mínimos con restricciones

Reduciendo variables

Primero consideramos el problema donde un mínimo con restricciones se puede obtener eliminando una variable:

De la función de restricción, consideramos una de sus variables como dependiente: $z (x, y) = a x + b y + c$
Esto nos deja una función $f$ de dos variables $f (x, y, z (x, y))$ , en la que podemos buscar extremos de la forma que ya sabemos

Método de multiplicadores de Lagrange

$ Los valores extremos de la función $f (x, y, z)$ (con las variables restringidas a $g (x, y, z) = 0$ ) se encuentran sobre la superficie $g = 0$ y en los puntos donde $\nabla f = λ \nabla g$
- Llamamos a $λ$ el multiplicador de Lagrange

TEOREMA 12: Teorema del gradiente ortogonal

Sea $f (x, y, z)$ derivable en una región que contiene una curva $C : \vec{r} (t) = g (t) \hat{i} + h (t) \hat{j} + k (t) \hat{k}$
Si $P_{0} \in C$ tal que $f (P_{0})$ es extremo local, relativo a sus valores sobre $C$
Entonces $\nabla f ⊥ C$ en $P_{0}$

Lo que hace este teorema es darnos una relación entre ambos gradientes, con la que podemos plantear un sistema de ecuaciones y deducir las coordenadas de los puntos críticos
Método de los multiplicadores de Lagrange:
- Si $f (x, y, z)$ tiene valores extremos sobre la superficie de nivel $g (x, y, z) = k$
- Si $\nabla g \neq 0$
1. Determinar todos los valores de $x, y, z, λ$ tal que: $\begin{matrix} \nabla f = λ \nabla g \\ g (x, y, z) = k \end{matrix}$
2. Evaluar $f$ en los puntos $(x, y, z)$ hallados, y tomar los valores extremos de entre estos

Dos restricciones

Si a $f$ restringida en $g_{1}$ la volvemos a restringir en una $g_{2}$ , podemos seguir aplicando el teorema 12 agregando otro multiplicador de Lagrange: $μ$
- Si $g_{1}, g_{2}$ son derivables
- Si $\nabla g_{1} ∦ \nabla g_{2}$
- La igualdad queda:
- $\begin{matrix} \nabla f = λ \nabla g_{1} + μ \nabla g_{2} \\ g_{1} (x, y, z) = 0 \\ g_{2} (x, y, z) = 0 \end{matrix}$
Por lo general, las tres funciones se cortan en una curva suave $C$ , y lo que buscamos son los puntos sobre esta curva donde el valor de $f$ es extremo
- En estos puntos, $\nabla f ⊥ C$ , pero $\nabla g_{1}, \nabla g_{2} ⊥ C$ también debido a que $C \in$ las superficies de las ecuaciones $g_{1, 2}$
- Por lo tanto, $\nabla f ∥ \nabla g_{1} ∥ \nabla g_{2} ⟹ \nabla f = λ \nabla g_{1} + μ \nabla g_{2}$
- Por estar sobre las superficies, los puntos también deben satisfacer $g_{1} = 0 \land g_{2} = 0$