Tratamiento de datos

@ [Simbología]

Conceptos básicos

Definir características de interés y conjunto para que se buscan conclusiones
Población: Conjunto de todos los elementos bajo estudio / Universo de objetos a los que se busca conclusiones
- Sería como "todos los objetos que existen, de la clase que tiene los atributos que debo estudiar"
- De esta forma puede ser todos los objetos del mundo, pero todos los objetos que me interesa estudiar
- @ $N$ (infinita), $n$ (finita)
Unidad elemental: Es un elemento de la población
Variable: es una característica de la unidad elemental
- Puedo pensarla como un field de un objeto; no es el valor, si no la característica en sí
- Tipos: cualitativa/categórica, cuantitativa (discreta, continua)
- @ Letras mayúsculas (variable), Letras minúsculas (valor)

Example

Población de dispositivos de almacenamiento:
Variable de interés: $X$ : capacidad real del dispositivo (GB)
Valor de una variable de una unidad: Uno de los dispositivos analizados presentó una capacidad real de 31,7Gb --> $x = 31, 7 G b$

Parámetro: Una medida que resume información de la población
- @ Letras griegas $π, μ, \dots$
Estadístico: Una medida que resume información de una muestra
Un estudio puede ser muestral o poblacional:
- Censo exhaustivo: Estudio que analiza todos los elementos de la población
- Estudio por muestreo: Analiza un subconjunto

Análisis descriptivo

Representaciones (Distribuciones de frecuencia y gráficos)

Frecuencia absoluta: $n_{k}$
- La sumatoria siempre es igual a $N$ (cantidad de observaciones)
Frecuencia relativa: $f_{k}$
- La sumatoria siempre es igual a $1$ (100% de las observaciones)
Frecuencia absoluta acumulada: $N_{k}$
Frecuencia relativa acumulada: $F_{k}$

Variables cualitativas

Gráfico circular
Gráfico de barras
Diagrama de pareto
- ~ Ilustra bien la ley de Pareto: La mayoría de los errores se deben a una minoría de las causas
- Es un diagrama de barras ordenado de mayor a menor
- Se añade también una línea que representa el porcentaje acumulado entre las categorías

Variables cuantitativas discretas

Diagrama de puntos
Gráfico de bastones
- Es como un gráfico de barras pero con columnas finitas
Diagrama de tallo y Hoja
- ~ Apropiado para conjuntos de datos pequeños
- Hoja: Es el último dígito
- Tallo: Es el resto de los dígitos
- & Ej.: $x = 148 GB ⟹ tallo = 14, hoja = 8$
#Boxplot

Variables cuantitativas continuas

Gráficas de serie de tiempo
- ~ Los gráficos anteriores no tienen en cuenta la diferencia de tiempo entre muestras, que podría ser una medida importante
- ! Puede ser importante hacerlo ANTES que un análisis de frecuencia
- Serie de tiempo: Conjunto de datos donde las observaciones se registran en el orden en el que ocurrieron
- Un serie de estas se grafica así:
  1. El eje horizontal representa el tiempo
  2. El vertical, el valor observado (sea $X$ )
Histograma
- Es como un gráfico de barras, que cuenta la frecuencia de un intervalo de clase
- Se puede añadir un polígono de frecuencias
  - Líneas unidas al punto medio de la cima de cada barra
Polígono de frecuencias acumuladas
#Boxplot

Medidas características de una muestra

Estadístico o parámetro (correspondiente para una muestra o población): Es un dato que resume información de una distribución de frecuencias o un conjunto de datos
- & Por ejemplo, el "promedio" es una medida que indica el centro de la distribución
Las medidas se categorizan según la información que dan

Medidas de posición

Estadísticos de tendencia central: Indican el centro de la distribución
- Media aritmética: $\overset{―}{X}$ es el promedio de las observaciones
  - $\overset{―}{x} = \frac{\sum_{i = 1}^{n} x_{i}}{n} = \sum_{i = 1}^{r} x_{i} f_{i}$
  - $x_{i}$ será el valor del punto medio de cada intervalo de clase, si los hubiera
  - El parámetro es representado por $μ$
  - Muy sensible a los valores extremos
- Moda: $\hat{X}$ es el valor de la variable con mayor frecuencia
  - Algunos conjuntos de observaciones no poseen moda (todos los valores son iguales ~ ?) o son bimodales (dos modas)
- Medidas de orden: Son aquellas que se definen con observaciones ordenadas en orden creciente ~ ????
  - Mediana: $\tilde{X}$ es el valor mínimo de la variable que acumula $\geq 50 %$ de las observaciones
    - Es el valor de la variable aleatoria
    - $\tilde{X} = min (x / F (x) \geq 0, 5)$
    - Si la cantidad de datos ordenados es impar, se toma como mediana el promedio de los dos valores centrales (es uno solo si es impar)
    - No es sensible a los valores extremos, sino más a los centrales
  - Cuartiles: $q_{1}, q_{2}, q_{3}$ son los mínimos valores que acumulan $\geq 25 %, 50 %, 75 %$ respectivamente de las observaciones
  - Percentiles: $p_{1}, p_{2}, \dots, p_{99}$ son los mínimos valores que acumulan el $1 %, 2 %, \dots, 99 %$ de las observaciones
Asimetría
- La asimetría la marca la "cola" de la distribución
- O sea, los valores extremos alejados y menos frecuentes

Medidas de dispersión

Son valores que representan cuánto se alejan del valor central las medidas en general

Rango: Diferencia entre los valores mayor y menor (vemos los puntos extremos)
- ~ Útil para ver la variación en un set de datos pequeño
Varianza $s^{2}$ : Es el desvío promedio de los datos respecto a la media
- ~ Útil para medir la precisión de un conjunto de medidas
- En otras palabras: es el promedio de (los cuadrados de) las diferencias de los datos respecto a la media de la muestra
- $s^{2} = \frac{1}{n - 1} \sum_{i = 1}^{n} (x_{i} - \overset{―}{x})^{2}$ ¿Por qué esta fórmula?
Desviación estándar $s$ ó $S D$ : Como la varianza toma los cuadrados de las desviaciones, deshacemos este efecto calculando la raíz cuadrada positiva de la varianza
- ~ Esta SÍ la podemos pensar como una distancia promedio de las observaciones con la media
- $s = \sqrt{s^{2}} = \sqrt{\frac{1}{n - 1} \sum (x_{i} - \overset{―}{x})}$

Regla empírica

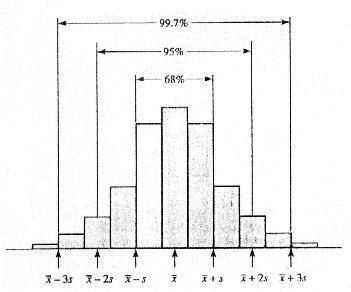
Si la distribución es simétrica y campanular, se establece que la mayoría de los datos de un conjunto se encuentran dentro de ciertos intervalos al rededor de la media.
Estos intervalos se construyen sumando y restando un múltiplo de la SD a la media

68% -> 1x SD respecto a la media
95% -> 2x SD respecto a la media
99.8% -> 3x SD respecto a la media

Pasted image 20240530192431.png

Coeficiente de variación $C V$ : Es el cociente entre la SD y la media aritmética
- Se interpreta: es la desviación estándar medida en unidades de la media (es un porcentaje de la media)
- Es el porcentaje de variación $(0 \leq C V \leq 1)$ . Multiplicar por 100 para tener el porcentaje
Rango/Recorrido intercuartil $r i q$ : Es la diferencia entre el tercer y primer cuartil
- ~ Recordando: sería la diferencia entre el primer valor que aparece el 25% de las veces y el primer valor que fue medido el 75% de las veces
- $ Esta medida no está influenciada por valores extremos
- Es la mejor medida de dispersión cuando se usa la mediana $(Q_{2})$ como medida de posición
- $R I = (Q_{3} - Q_{1})$

Por qué la varianza se calcula así?

Cuando usamos la media aritmética, nos interesa definir también la variabilidad promedio entre los datos y el promedio de la muestra.
Pero surge el problema de que este promedio resulta $= 0$ :
$\sum_{i = 1}^{n} (x_{i} - \overset{―}{x}) = 0$
Por lo tanto, definimos la varianza haciendo el promedio del cuadrado de estos "desvíos".
Además, por razones pendientes de explicación ~ (es el SD muestral), se resta 1 a $n$ . La ecuación modificada queda:
$\frac{1}{n - 1} \sum_{i = 1}^{n} (x_{i} - \overset{―}{x})^{2}$

Outliers (valores anómalos)

Podemos pensar, a partir de la regla empírica, que un valor es anormalmente extremo (muy grande o muy chico) si su desviación de la media es 3 veces mayor que la SD.

$ $x - \overset{―}{x} > 3 \cdot s ⟹ x es outlier$

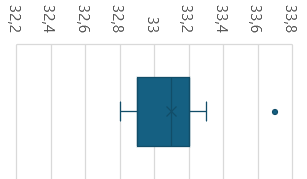
Boxplot

Usando: Los 3 cuartiles y los 2 valores extremos (máximo y mínimo)
Podemos obtener un gráfico que resume muy bien los datos
1. Marcamos los cuartiles (y cerramos la caja)
  - Así queda una caja con la Mediana marcada
2. Luego se marcan los puntos extremos y se extienden los "bigotes" desde los laterales de la caja
& Ej:
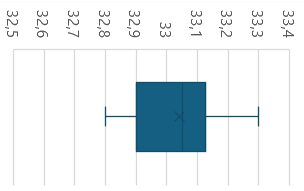
Para una interpretación más útil, podemos redefinir los valores extremos (de los bigotes) de la siguiente forma:

{\begin{cases} v_{m} = Q_{1} - 1.5 RI \\ v_{M} = Q_{3} + 1.5 RI \end{cases}

Y luego, marcamos las observaciones fuera de este rango como outliers
& Ej: