Potencial Eléctrico

Recordamos la ley de Coulomb. Además, la fuerza eléctrica es conservativa. Entonces existe una función energía potencial $V$ asociada a la fuerza eléctrica.
La energía potencial por cada unidad de carga es una función de la posición de la carga, la llamamos Potencial eléctrico y la medimos en Joules/Coulomb = Volt.
Tip: En muchos casos es más fácil que calcular el campo eléctrico porque es un campo escalar

Diferencia de potencial

Es la cantidad de trabajo requerida para mover una unidad de carga hasta un punto del campo $\vec{E}$
- En el caso de un sistema de cargas puntuales es el trabajo para mover la carga respecto al infinito (donde no hay campo)

d V = \frac{d U}{q_{0}} = - \vec{E} \cdot d \vec{l}

Es el negativo del trabajo realizado por el campo eléctrico sobre una carga cuando esta se desplaza de un punto $a$ a $b$ $$\Delta V = V_b - V_a = {\Delta U \over q_0}= -\int_a^b\vec E\cdot d\vec l$$
El campo escalar de potencial eléctrico es continuo en todos los puntos del espacio (salvo justo donde hay una carga puntual o una línea de carga, donde es infinito)
Lo único que importa del potencial es la variación, por lo que podemos elegir que sea cero donde nos convenga
- Esto nos permite elegir un punto donde la energía potencial sea igual al potencial eléctrico y relacionarlo de forma que $U = q_{0} V$
Las líneas de campo indicarán en qué dirección se acelera una carga que se coloca en el campo
- Siempre apuntan la dirección en la que $E$ disminuye más rápido
- Se puede decir que la unidad de $E$ es la velocidad con la que cambia V según la distancia, y la unidad es $E = 1 N / C = 1 V / m$ (volt por metro)

Potencial debido a un sistema de cargas puntuales

El potencial debido a una carga puntual es $$V={kq\over r}-{kq\over r_{ref}} \space [23.7]$$
- Estos son puntos arbitrarios (que nos convienen), entonces podemos elegir que el punto de referencia sea el infinito, donde el potencial es $0$ : $$V={kq\over r}\space [23.8]$$ y esto es el potencial de Coulomb
El trabajo necesario para llevar una carga $q_{0}$ desde el infinito hasta una distancia $r$ de la carga puntual es $k q_{0} q / r$
Decimos que dos cargas no interaccionan si la energía potencial del sistema que componen es cero
- Esto se da cuando están infinitamente separadas

Calcular $\vec{E}$ a partir de $V$

~ Recordar que el campo no cambia cuando la carga testigo se mueve perpendicularmente al campo $\vec{E}$
Dado que el campo $\vec{E}$ indica la dirección y magnitud del cambio de potencial $V$ , podemos relacionarlos de la forma: $$\vec E_x = - {dV(x)\over dx}; \vec E_r = -{dV(r)\over dr}$$
- $E$ es el opuesto al gradiente del potencial $V$

Calcular $V$ para distribuciones continuas de carga

Simple: Se considera el $V$ de un trozo de carga $d q$ y se integra $$V=\int{k\space dq\over r}$$
- Es necesario que $V = 0$ en el infinito, por lo que esto no funciona para distribuciones de carga lineal infinita o de plano de carga infinito

Anillo cargado

~ note to self: No hace falta integrar respecto al ángulo. Lo único que no es cte. es $d q$ y se integra en $[0, Q]$ . Entonces $\int_{0}^{Q} d q = Q$ 🤦‍♂️

V = \frac{k Q}{r} = \frac{k Q}{\sqrt{x^{2} + a^{2}}} = \frac{k Q}{| x |} \frac{1}{\sqrt{1 + (a^{2} / x^{2})}} [23.20]

Disco cargado

Consideramos la figura como una serie de anillos concéntricos de radio $a$ y anchura $d a$
- El área será $2 π a d a$

V= 2\pi k\space\sigma |x| \cdot(\sqrt{1+{R^2\over x^2}}-1)\space [23.21]$$ donde $R$ es el radio del *disco*  ### Potencial respecto a una corteza esférica de carga ![Pasted image 20231127192411.png](/img/user/Im%C3%A1genes/Pasted%20image%2020231127192411.png) - **Afuera de la esfera** ($r\geq R$) 	- Se comporta como una carga puntual $$V_P = {kQ\over r}

Dentro de la esfera el potencial no cambia porque $\vec{E} = 0$ , pero pasando el umbral de $r = R$ , el potencial cae según la función anterior

V_{P} = \frac{k Q}{R} (cte.)

$V$ para distribuciones infinitas de carga

Las fórmulas derivadas anteriormente no funcionan para este caso (porque tomábamos el potencial respecto a $x = \infty$ )

Plano infinito de carga

Consideramos el caso de un disco donde su $R \to \infty$
Se calcula primero el campo $E$ , y de ahí se deriva el potencial

V = V_{0} - 2 π k σ | x |

Donde $V_{0}$ es el valor del potencial de un punto de referencia

Carga lineal infinita

Derivado de la función de $\vec{E}$ para situaciones similares, el potencial es:

V = - 2 k λ \ln \frac{R_{r e f}}{R}

siendo $R_{r e f}$ una distancia de referencia arbitraria desde el conductor, entre $0 < R_{r e f} < \infty$

Superficies equipotenciales

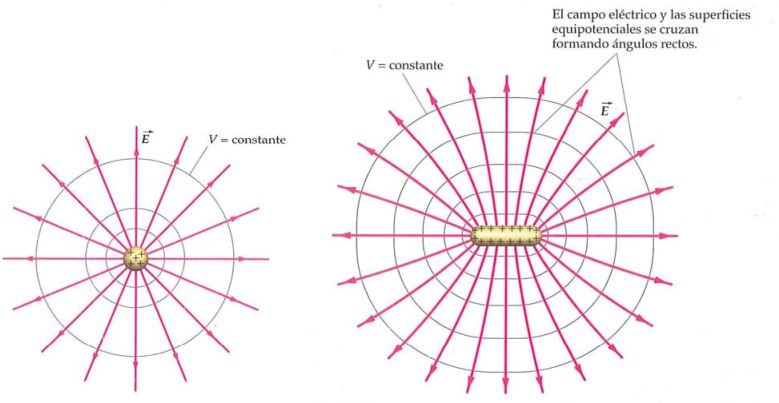
Pasted image 20231128082053.png

Cualquier línea de campo $\vec{E}$ que atraviese una superficie equipotencial deberá ser perpendicular a esta
El potencial entre dos conductores depende de sus formas geométricas
- Cuando se conectan, se comportan como un solo conductor

Repasos pendientes

Cap 23.2

! Revisar la derivación del potencial de Coulomb (por si la práctica pide hacerla)
- Sale por la integral, no preguntes

Cap 23.3

"Si el desplazamiento $d l$ es perpendicular al campo $\vec{E}$ , $d V = 0$ " (pág. 674)
- ? En el ejercicio 8 de electrostática la carga se mueve perpendicularmente al campo, no efectúa un trabajo eso?
  - & Sí, pero el trabajo se realiza en el eje Y. No hay trabajo en la componente X

Cap 23.4

& Ejemplo 23.12

Cap 23.5

& Ejemplo 23.13

Anexos

Unidades

El producto de la unidad de carga $e$ de un electrón por un Voltio es el eV (electrón-Voltio), una unidad de energía usada en física atómica ( $1.6 \cdot 10^{- 19} J$ )