Integrales Iteradas

Para integrar funciones de una variable, se parte el intervalo finito en pequeños subintervalos, multiplicando el ancho de cada uno por el valor de $f$ en un punto $c_k$ dentro de este subintervalo, y luego se suman los productos. Algo similar sucede para las integrales dobles

Integrales dobles

• Consideramos una función $f(x,y)$ definida en una región rectangular $R$ $$R: a\leq x \leq b, \space c\leq y\leq d$$
• Norma de una partición P $|P|$: Es el mayor de las alturas/anchuras
• La suma de Riemann para dos variables es

• Cuando existe el límite de las sumas $S_n$ para cualquier número de $P$, es porque se obtiene el mismo valor sin importar las elecciones que se hagan, y $f$ es integrable
• Al límite se le conoce como integral doble de $f$ sobre $R$:

• @ Si $f$ es continua en $R$, $f$ es integrable

Interpretación geométrica

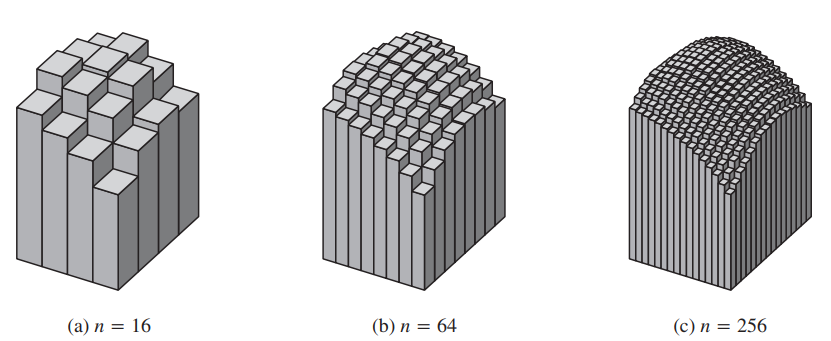
• Cuando $f(x,y)$ es una función sobre la región R del plano $xy$, podemos interpretar la integral doble de $f$ en $R$ como el volumen de la región sólida tridimensional en el plano $xy$ acotada por $R$ y la superficie $z=f(x,y)$
• Cada término $f(x_k,y_k)\mathrm{\Delta }{A}_k$ en la suma $S_n=\sum f(x_k,y_k)\mathrm{\Delta }{A}_k$ es el volumen de una caja rectangular vertical
• El volumen se define como

Teorema de Fubini para integrales dobles

• Integral iterada/repetida: Es una expresión de la forma:
  • ${\displaystyle V={\int }_a^b{\int }_c^{d}f(x,y)dydx}$
  • Dice que para obtener, por ej. el volumen, se integra $f(x,y)$ primero respecto a $y$ en $y=c\to y=d$, manteniendo $x$ fija. Luego se integra ese resultado respecto de $x$ en $x=a\to x=b$.
  • Los límites de integración $c,d$ se asocian a $y$ de forma que se colocan en la integral más cercana a $dy$
  • El teorema de Fubini dice que no importa el orden de integración

![Note] Caso particular para funciones producto -
En el caso de que $f$ se pueda expresar como $f(x,y)=g(x)\cdot h(y)$, se puede simplificar la integral doble de la siguiente forma:

$${\iint }_{R}g(x)h(y)dA={\int }_a^{b}g(x)dx{\int }_c^{d}h(y)dy$$

Integración sobre regiones generales

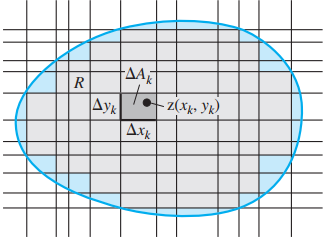
• Estas regiones también se integran con integrales dobles, pero el problema yace en la definición de sus límites, ya que no son simples segmentos paralelos a los ejes
  • Frecuentemente definiremos estos límites usando variables, no constantes

Regiones acotadas no rectangulares

• La suma de Riemann se analiza de la misma forma, pero considerando los términos donde la subdivisión está completamente contenida en la región
• La naturaleza de la frontera de $R$ introduce algunos aspectos:
  • Cuando $R$ tiene frontera curva, los $n$ rectángulos de una partición están dentro de $R$, pero no la cubren del todo
  • La propiedad de ser "casi completamente cubierta" por una partición de norma ínfima se cumple por todas las regiones que estudiamos
    • Polígonos y elipsoides OK, Curvas fractales oh shit

Volúmenes

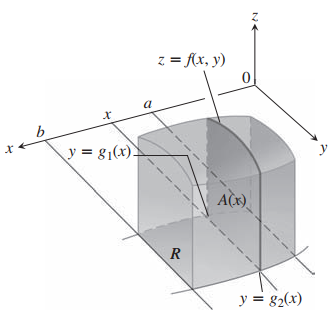
• Si la región $R$ está acotada por curvas $y=g_1(x),y=g_2(x)$ por abajo y arriba respectivamente, y por rectas $x=a,x=b$ a los lados, cortamos el volumen en rodajas
  1. Calculamos el área de la sección transversal $$A(x)=\int_{y=g_1(x)}^{y=g_2(x)} f(x,y)\space dy$$
  2. Y luego integramos $A(x)$ $$V=\int_a^b A(x)\space dx = \int_a^b\int_{y=g_1(x)}^{y=g_2(x)} f(x,y)\space dy\space dx$$
• De manera similar, si las funciones $x=h_1(y),x=h_2(y)$ son cotas por izquierda y por derecha, el volumen lo define la integral iterada $$V=\int_c^d\int_{h_1(y)}^{h_2(y)} f(x,y)\space dx\space dy$$

• @ Si bien no importa el orden de integración (respecto de $x$ o de $y$), hay algunas funciones más fáciles de integrar primero respecto de una variable que de otra, por ejemplo: $$\int_0^1\int_0^x {\sin x\over x}dy\space dx {\color{gray}\text{ es más fácil que: }} \int_0^1\int_y^1{\sin x\over x}dx\space dy$$

Definir los límites de integración

Podemos usar un procedimiento para determinar casi cualquier límite de integración. Los que no se puedan averiguar con este método se pueden dividir hasta que este funcione

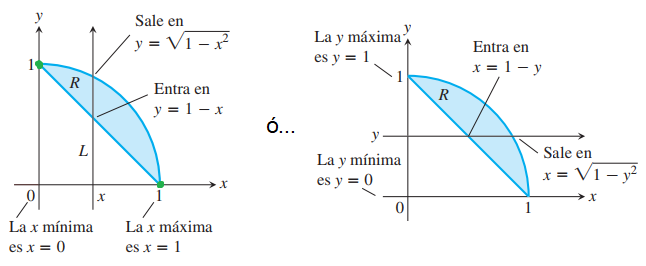
• Uso de transversales verticales
  • Cuando tenga que evaluar ${\iint }_{R}f(x,y)dA$, integrar primero respecto a $y$ y después respecto a $x$:
  1. Graficar la región $R$ en el plano
  2. Identificar desde abajo hacia arriba las funciones $g(x)$, estas son las cotas verticales
  3. Las cotas laterales son las intersecciones de estas funciones
• Uso de transversales horizontales
  • Para calcular el orden inverso de integración, usamos rectas horizontales en el paso 2 y 3

Propiedades de las integrales dobles

• Si $f(x,y),g(x,y)$ son continuas en la frontera de la región $R$

• Entonces:

  1. Múltiplo cte.: ${\iint }_{R}c\cdot fdA=c\cdot {\iint }_{R}fdA$
  2. Suma y resta: La integral de la suma, es igual a la suma de las integrales
  3. Dominación 😈
     1. ${\iint }_{R}f(x,y)dA\ge 0$ si $f(x,y)\ge 0$ en $R$
     2. ${\iint }_{R}f(x,y)dA\ge {\iint }_{R}g(x,y)dA$ si $f(x,y)\ge g(x,y)$ en $R$
  4. Aditividad:
     • Si $R=R_1\cup R_2/R_1\cap R_2=\mathrm{\varnothing }$
     • Entonces ${\iint }_{R}fdA={\iint }_{R_1}fdA+{\iint }_{R_2}fdA$

• Si $f(x,y)\ge g(x,y)\mathrm{\forall }(x,y)\in D$

• Entonces: ${\iint }_{D}f(x,y)dA\ge {\iint }_{D}g(x,y)dA$

Áreas por doble integración

Podemos usar las integrales dobles para calcular el área de regiones acotadas en el plano, y para determinar el valor promedio de una función de dos variables

Área de regiones acotadas en el plano

• Consideramos la función/curva de nivel $f(x,y)=1$ en la definición de integral doble sobre región R: $$S_n=\sum_{k=1}^n f(x_k, y_k) \Delta A_k = \sum_{k=1}^n\Delta A_k$$
  • Esto aproxima el área total de la partición de $R$, por lo que podemos calcular el límite $$\lim_{|P|\to0}\sum_{k=1}^n\Delta A_k = \iint_R dA$$

Valor promedio

• La integral de una $f$ de dos variables es: La integral sobre la región $R$, dividida entre el Área de $R$