Integrales en coordenadas polares

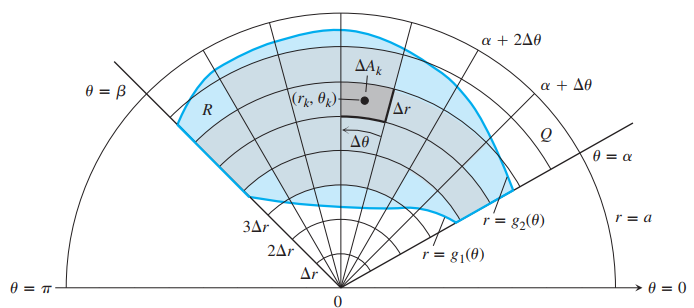
Pasted image 20240126085253.png
Si tenemos una región de esta forma, dividimos a Q con una malla de arcos (circunferencias concéntricas al origen) con radios $m Δ r ⟹ Δ r = a / m$ , y rayos dados por $θ = α + m^{'} Δ θ ⟹ Δ θ = (β - α) / m^{'}$

Las divisiones se llaman rectángulos polares
- El factor de área infinitesimal de cada rectángulo polar, al hacer el cambio de variable, debe reemplazarse por el Determinante Jacobiano, por lo tanto: $$S_n=\sum_{k=1}^n f(r_k,\theta_k)r_k\Delta r \Delta\theta$$ $$\lim_{n\to\infty} S_n = \iint_R f(r,\theta) r\space dr\space d\theta$$
Existe el teorema de Fubini para las integrales en coordenadas polares: $$\iint_Rf(r,\theta)dA = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=g_1(\theta)}^{r=g_2(\theta)}f(r,\theta)\space r\space dr\space d\theta$$

Área en coordenadas polares

Si $f$ es una función constante $f (r, θ) = 1$ , el área de una región cerrada y acotada $R$ en el plano de coords. polares es $$A=\iint_Rr\space dr\space d\theta$$

Cambio a coordenadas polares en una integral doble

En resumen:

Si $f$ continua en un rectángulo polar $R$ dado por $0 \leq a \leq r \leq b, α \leq θ \leq β$
- Mientras que $0 \leq β - α \leq 2 π$ (mientras que el área sea una revolución o menos)
Entonces: $$\iint_R f(x,y)dA = \int_\alpha^\beta\int_a^b f(r\cos\theta,\space r\sin\theta)\cdot r\space dr\space d\theta$$

Si $R$ está dada por $R = {(r, θ) | α \leq θ \leq β, h_{1} (θ) \leq r \leq h_{2} (θ)}$
Entonces: $$\iint_R f(x,y)dA = \int_\alpha^\beta\int_{h_1(\theta)}^{h_2(\theta)}f(r\cos\theta, \space r\sin(\theta))\cdot r\space dr\space d\theta $$

Determinar los límites de integración