Integrales Dobles
- La región de integración representa un área del plano
ahora - Trabajamos con una función tridimensional
- Es decir, para cada punto del plano
, existe un número real (la altura de la superficie en ese punto) 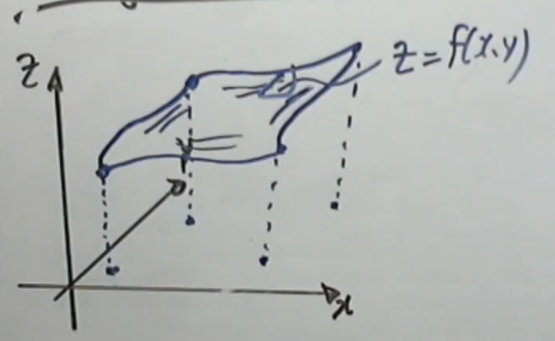
- Es decir, para cada punto del plano
- Al proyectar esta superficie al plano
obtenemos el dominio - Llamamos
a este dominio de integración y lo dividimos en áreas diferenciales - La integral será entonces el volumen bajo la superficie de la función
, calculada con la siguiente suma de Riemann y simbolizada con una doble - Existen tres Casos de integración
Área con integrales dobles
Clase 15: ~