Cuando una partícula se mueve en el espacio, las coordenadas de cada punto de su trayectoria pueden ser descritas por funciones del tiempo: $x=f(t),y=g(t),z=h(t)⟹P(f(t),g(t),h(t))$.
A su vez, cada punto de la trayectoria se puede describir como un vector posición (desde el origen) $\overrightarrow{r}(t)=\overrightarrow{OP}=f(t)\hat{i}+g(t)\hat{j}+h(t)\hat{k}$

• Funciones componentes: Son $f,g,h$, quienes describen las componentes de un punto de la trayectoria para un momento del tiempo $t$ dado

• Curva trazada por $\overrightarrow{r}$: Es la trayectoria que recorre la partícula en un intervalo de tiempo $I$

  • Entendemos que $t\in I$

• Definimos entonces a $\overrightarrow{r}(t):R\to R^3$ como una función vectorial, con dominio Real y rango en el Espacio ($R^3$)

  • Estas funciones representan superficies en el espacio

• Función escalar: Una función con Dominio y Rango en $R$

Funciones vectoriales

Límites y continuidad

• Límite: El límite de la función vectorial $\overrightarrow{r}$ es igual al límite de de sus componentes $$\lim_{t\to t_0}\vec r(t) = (\lim_{t\to t_0}f(t))\hat i \space + (\lim_{t\to t_0}g(t))\hat j \space + (\lim_{t\to t_0}h(t))\hat k$$
• Continuidad: Una función vectorial $\overrightarrow{r}(t)$ es continua en un punto $t=t_0$ de su dominio, si $\underset{t\to t_0}{lim}\overrightarrow{r}(t)=\overrightarrow{r}(t_0)$. La función es continua si es continua en cada punto de su dominio
  • O sea, es continua si todas sus componentes son contínuas

Derivadas y movimiento

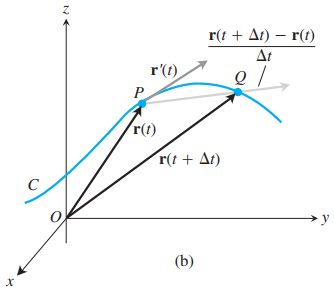
• Derivada: La derivada de la función vectorial $\overrightarrow{r}(t)$ se compone de las derivadas de las funciones componentes $$\vec r\space'(t) = f'(t)\hat i + g'(t)\hat j + h'(t)\hat k$$
  

Funciones vectoriales de magnitud constante

• Esto significa que la partícula tiene una trayectoria sobre una esfera
• Por lo tanto, la velocidad será siempre ortogonal al vector posición $(\overrightarrow{r}\perp \overrightarrow{v})$

Integrales de funciones vectoriales

• Definimos integral indefinida de una función vectorial $$\displaystyle\begin{matrix} \int\vec r(t)\space dt = \vec R(t) + \vec C\ \vec R(t) \text{ antiderivada de } \vec r(t) \iff {d\vec R\over dt} = \vec r \space \forall t \in I\end{matrix}$$
• Para integrar una función vectorial, se integra cada componente
• Del mismo modo se calculan las integrales definidas, integrando cada componente

Longitud de arco en el espacio

Se puede medir la longitud de una curva, desde un punto base de la misma, usando un factor de distancia dirigida $s$.

• La longitud $L$ de una curva suave cuando el parámetro $t$ varía en $a\to b$ es $$L = \int_a^b|\vec v| = \int_a^b\sqrt{(dx/dt)^2+(dy/dt)^2+(dz/dt)^2}\space dt$$
  • O sea, es la suma de los vectores velocidad en cada punto, pues $\overrightarrow{v}$ siempre apunta hacia adelante en la dirección hacia donde se dirige la curva
• Parámetro de longitud de arco $s$: $$s(t) = \int_{t_0}^t\sqrt{[x'(\tau)^2+y'(\tau)^2+z'(\tau)^2]}\space d\tau = \int_{t_0}^t|\vec v(\tau)|\space d\tau$$

Curvatura

• $\overrightarrow{T}$ es el versor asociado a la velocidad $\overrightarrow{v}$ ($\overrightarrow{T}=\overrightarrow{v}/|\overrightarrow{v}|$)
• Si $\overrightarrow{T}(t)$ es el versor perpendicular a la curva en cada tiempo $t$, la derivada $d\overrightarrow{T}/ds$ indica cuánto cambia la dirección de la curva en cada punto
• $ Curvatura $\kappa$: $$\kappa = |{d\vec T\over ds}| = {1\over|\vec v|}{d\vec T\over dt}$$
  • $\kappa$ es constante cuando la curva es una línea recta o una circunferencia
• Vector normal unitario principal $N$: Es el versor que apunta a la dirección en la que la curva se dobla. Es la derivada de $T$ $$\vec N = {1\over k}{d\vec T\over ds} = {d\vec T\over |d\vec T|}$$

Círculo de curvatura para curvas planas

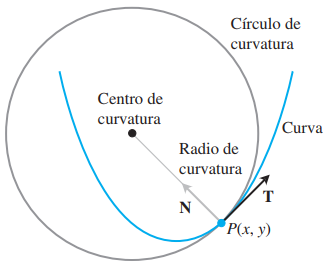
• Existe para todo punto sobre la curva donde $\kappa \ne 0$. Es el círculo en el plano de la curva que
  1. Tiene la misma recta tangente que la curva
  2. Tiene la misma curvatura que la curva en $P$
  3. Está del lado cóncavo de la curva
• El radio de curvatura de la curva en $P$ es: $\rho =1/\kappa$