Cilindros y superficies cuadráticas

Superficies cuadráticas: Son superficies definidas por ecuaciones de segundo grado en $x, y, z$
- Un ejemplo son las esferas

Cilindros

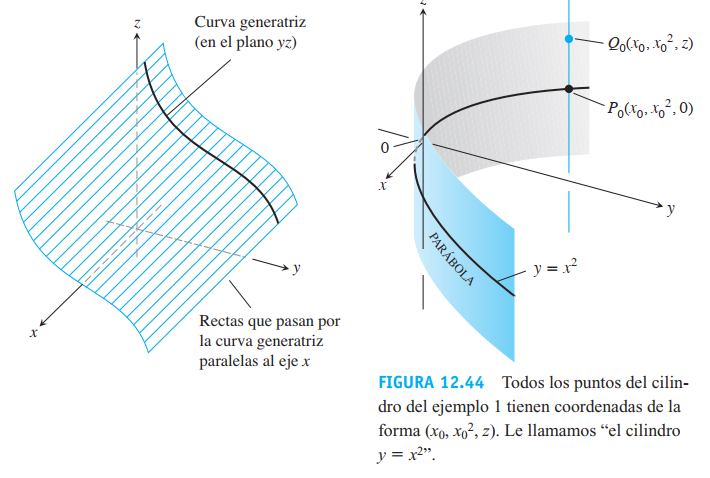
Pasted image 20231228003619.png

Es una superficie hecha del movimiento de una línea recta paralela a una recta fija a lo largo de una curva generatriz
En geometría sólida, esta curva generatriz es una circunferencia, dando la forma de tubo de toda la vida
Acá, permitimos que la curva sea de cualquier forma

Nombre	Fórmula	Imagen e inclinación
Elipsoide	$${x^2\over a^2}+{y^2\over b^2}+{z^2\over c^2}=1$$ Mismo signo, todas las variables exp. 2	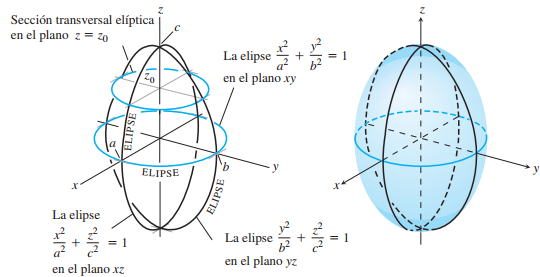Inclinación ppal. dirigida al eje de mayor coeficiente
Paraboloide elíptico	$${x^2\over a^2}+{y^2\over b^2}+{z\over c}=0$$ Una variable de exp. 1	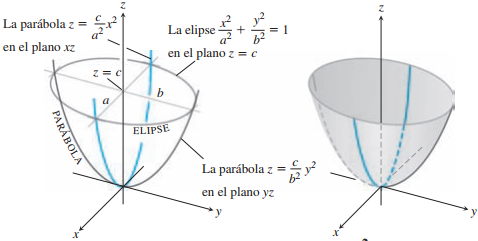Dirigida al eje de variable de exp. 1
Paraboloide hiperbólica	$${y^2\over b^2}-{x^2\over a^2}={z\over c}$$ Al menos una var. negativa	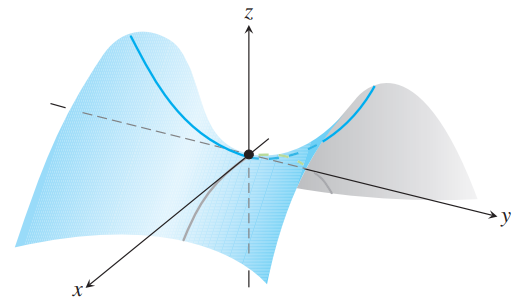Dirigida al eje de variable de exp. 1
Hiperboloide 1 hoja	$${x^2\over a^2}+{y^2\over b^2}-{z^2\over c^2}=1$$ Una variable negativa, igualado a uno	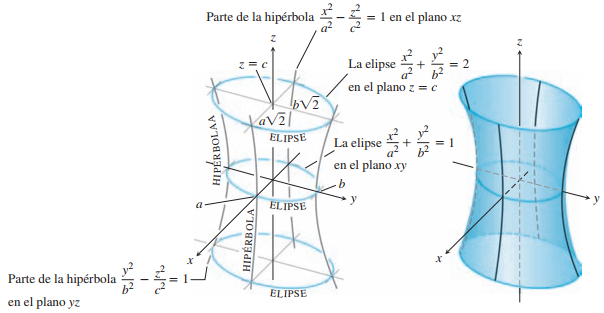El eje es de la variable negativa
Hiperboloide 2 hojas	$${z^2\over c^2}-{x^2\over a^2}-{y^2\over b^2}=1$$	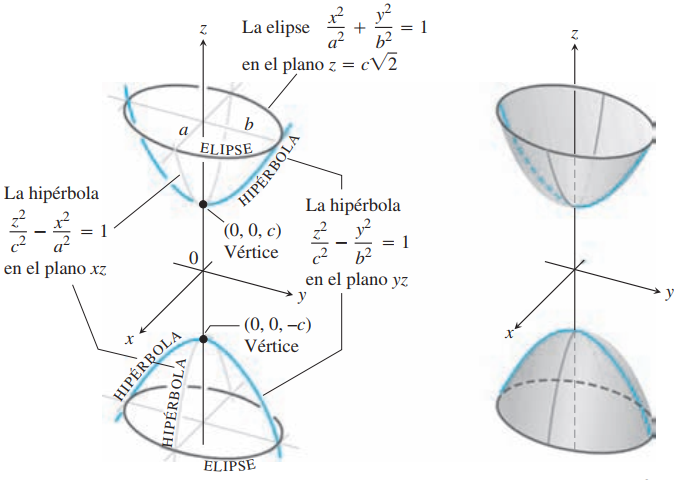El eje es el de la variable positiva
Cono	$${x^2\over a^2}+{y^2\over b^2}={z^2\over c^2}$$ $${x^2\over a^2}+{y^2\over b^2}-{z^2\over c^2}=0$$ Una variable negativa, igualado a cero	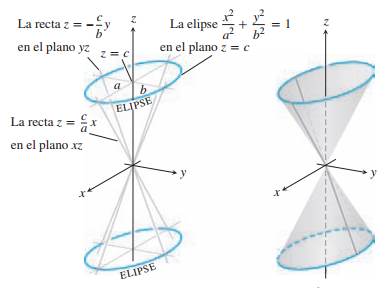El eje es el de la variable negativa

Pasted image 20231228154710.png

Cilindro: Inclinado hacia el eje ausente (coef. 0) en la ecuación
Elipsoide: La inclinación se da por los coeficientes, y se encuentra la inclinación hacia el eje de la variable de mayor denominador
Paraboloide elíptico/hiperbólico: El eje de simetría es el de la variable de exponente 1
Hiperboloide de 1 hoja: El eje es el de la variable negativa
- Cono: ídem
Hiperboloide de 2 hoja: El eje es el de la variable positiva