[Arriba:: Física MOC]
[Siguiente:: Fuentes de campo magnético]

Fuerza ejercida por un campo campo magnético

• Sobre cargas eléctricas puntuales móviles, un campo magnético $\overrightarrow{B}$ ejercerá una fuerza $$\vec F=q\space\vec v\times\vec B \space[T]$$
  • Las unidades de este campo son el Tesla $1T=1N/A\cdot m$, y el Gauss $1G={10}^{-4}T$
• Esto aplica también para conductores lineales llevando una corriente (pues la corriente no es más que un montón de cargas moviéndose juntas)
  • Si el cable es recto y el campo es uniforme $$\vec F=I\vec L\times\vec B$$
  • De lo contrario, calculamos diferenciales de fuerza $d\overrightarrow{F}$ respecto a diferenciales de longitud del cable $d\overrightarrow{l}$
  • Llamamos a $Id\overrightarrow{l}$ un elemento de corriente
• Las Líneas de campo $\overrightarrow{B}$ se diferencian de las líneas de campo $\overrightarrow{E}$ en que...
  1. Son perpendiculares a la fuerza magnética que generan
  2. Son cerradas (empiezan en el polo norte del imán y terminan en el polo sur)

Movimiento de una carga puntual

• La fuerza magnética sólo modifica la dirección de la velocidad de la partícula, nunca su módulo
  • El campo $\overrightarrow{B}$ no realiza trabajo sobre las partículas y no modifica su energía cinética
  • Una partícula moviéndose perpendicular a un campo describirá una trayectoria circular llamada ciclotrón
    • $ Calculamos el radio de la trayectoria desde la 2° ley de Newton $$F = ma \implies qvB = m{v^2\over r}$$
    • $ Periodo de ciclotrón: $$T={2\pi m\over qB}$$
    • La frecuencia es el inverso del periodo

Selector de velocidades

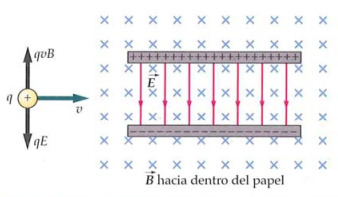
• Es un dispositivo que genera campos $\overrightarrow{E}$ y $\overrightarrow{B}$ cruzados (perpendiculares entre sí) de forma que sólo las partículas con cierto valor de $v$ salen disparadas de él
• Las dos fuerzas se equilibran si $F_E=F_B⟹qE=qvB⟹v=E/B$
  ~

Método de Thomson

Espectrómetro de Massas

Ciclotrón

Momentos de fuerza sobre espiras de corriente e imanes

• Definimos el vector normal $\hat{n}$ de una espira de portadora de corriente, como el vector unitario en dirección normal al plano de la espira, y con la dirección determinada por la regla de la mano derecha, siguiendo el sentido de la corriente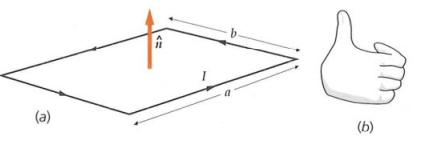
• Si $|\widehat{nB}|\ne 0°$, el campo magnético ejerce 4 fuerzas
  • 2 se cancelan (están sobre el eje de rotación)
  • 2 tienden a girar la espira: $F_1=F_2=IaB$
• ~ Definimos momento como $$\tau = NIAB\space\sin\theta$$ siendo $N$ el número de vueltas de la espira y $A$ el área la misma
  • Este momento tiende a girar la espira de forma que $\hat{n}$ tenga la misma dirección que $\overrightarrow{B}$, para que el plano sea perpendicular al campo
• $ El momento puede escribirse también en función del momento dipolar magnético $\mu$ (momento magnético) $$\vec\mu = NIA\space\hat n \space[A\cdot m^2]$$
  • $ Ahora sí escribimos el momento de fuerza de la espira $$\vec\tau=\vec\mu\times\vec B$$

Energía potencial de un dipolo magnético

• Cuando un momento $\tau$ actúa sobre un objeto y este gira, se realiza un trabajo $$dW = -\tau\space d\theta = -\mu B\sin\theta \space d\theta$$
  • El signo menos tiende a disminuir $\theta$
  • Relacionamos el trabajo con la disminución de energía potencial
  • $ Si elegimos la energía potencial para que sea cero cuando $\theta =90(U_0=0)$, la energía potencial del dipolo es $$U=-\mu B\cos\theta \color{red} = -\vec\mu\cdot\vec B$$

Anexos

• $ Momento magnético para un disco cargado en rotación $$\vec\mu = {1\over 4} \pi\sigma R^4\vec\omega$$

Resumen

• Fuerza magnética
  • Sobre una carga: $\overrightarrow{F}=q\overrightarrow{v}\times \overrightarrow{B}[T]$
  • Sobre un elemento de corriente: $d\overrightarrow{F}=Id\overrightarrow{l}\times B$
• Movimiento de cargas puntuales
  • Una partícula de masa $m$ y carga $q$ moviéndose a velocidad $\overrightarrow{v}$ perpendicular a un campo $\overrightarrow{B}$ tiene una trayectoria circular
  • El periodo y frecuencia son independientes del radio de la órbita o la velocidad
  • 2° ley de Newton: $F=m\overrightarrow{a}⟹qvB=m\frac{v^2}{r}$
    • Permite despejar el radio de la trayectoria
  • Periodo de ciclotrón: $T=\frac{2\pi m}{qB}$
  • Frecuencia: $1/T$
  • Selector de velocidades: Un dispositivo que genera campos $\overrightarrow{E}$ y $\overrightarrow{B}$ cruzados de forma que sólo las partículas con cierto valor de $v$ salen disparadas de él
    • $E=vB$
• Espiras de corriente
  • Momento magnético: $\overrightarrow{\mu }=NIA\hat{n}$
  • Momento de fuerza magnética: $\overrightarrow{\tau }=\overrightarrow{\mu }\times \overrightarrow{B}$
  • Energía potencial: $U=-\overrightarrow{\mu }\cdot \overrightarrow{B}$