Campo Eléctrico. Distribuciones contínuas de carga

Densidad de carga

Densidad de carga volumétrica ( $ρ$ ): $ρ = \frac{Δ Q}{Δ V}$
Densidad de carga superficial ( $σ$ ): $σ = \frac{Δ Q}{Δ A}$
Densidad de carga lineal ( $λ$ ): $λ = \frac{Δ Q}{Δ L}$

Todas las fórmulas aquí son derivadas de la ley de Coulomb, integrando diferenciales de campo (

d \vec{E}

) causados por trozos de las cargas totales (

d q

)

$d \vec{E} = \frac{k \cdot d q}{r^{2}} \hat{r} ⟹ \vec{E} = \int_{V} \frac{k \cdot d q}{r^{2}} \hat{r}$

Campo eléctrico causado por...

Una carga lineal finita

Sobre el eje x

E_{x} = \frac{k Q}{x_{P}^{2} - (\frac{L}{2})^{2}}, x_{P} > \frac{L}{2} [22.5]

Si x_{P} >> L ⟹ \vec{E} \approx \frac{k Q}{x_{P}^{2}}

Sobre el eje y (sobre la mitad del segmento)

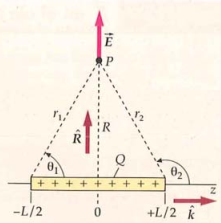
Pasted image 20231122183532.png

Revisar las Identidades trigonométricas
Usamos ecuaciones 22.8 y reemplazamos $x_{1}$ y $x_{2}$ , de modo que no sean infinitos
Los ángulos van a ser iguales
- y: Luego se reemplaza el $2 \sin (ϕ)$ en función de $L$ e $y$
- x: La diferencia de cosenos da 0 y cancela toda la componente

\vec{E} = \frac{k λ}{y} \cdot 2 \frac{L / 2}{\sqrt{(L / 2)^{2} + y^{2}}} \hat{j}

Fuera del eje

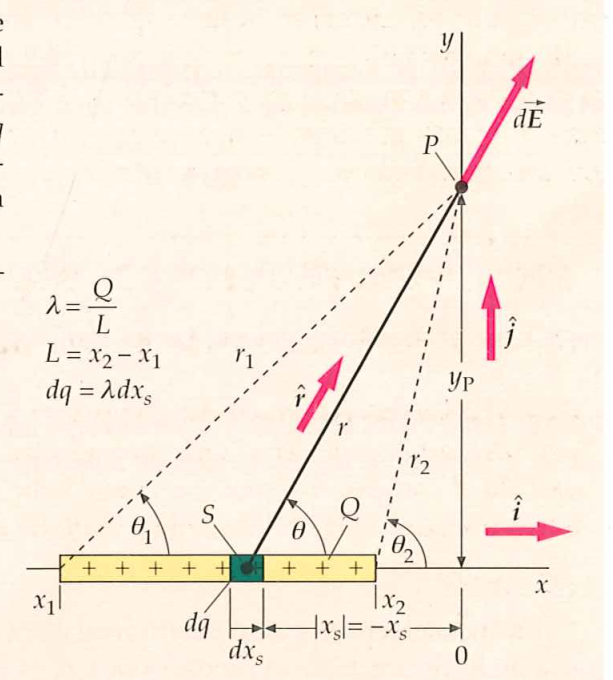
Pasted image 20231122115413.png

Componente y: {\vec{E}}_{y} = \frac{k λ}{y} (\sin ϕ_{2} - \sin ϕ_{1}) = \frac{k Q}{L y} (\sin ϕ_{2} - \sin ϕ_{1}) [22.8a]

Componente x: {\vec{E}}_{x} = \frac{k λ}{y} (\cos ϕ_{2} - \cos ϕ_{1}) = \frac{k Q}{L y} (\cos ϕ_{2} - \cos ϕ_{1}) [22.8b]

Una carga lineal infinita

- Calculamos el límite de las ecuaciones 22.8 cuando $(\phi_1\to-\pi /2; \phi_2\to\pi /2)$ - Esto corresponde a $(x_1\to-\infty; x_2\to\infty)$, o sea que la carga parece ser infinitamente larga - Obtenemos que $E_x = 0 \text{ (cte.)}, E_y={2k\lambda / y}$: $$E_y = \frac{2k\lambda}{y} \text{ [22.9]}$$ donde $y$ es la distancia de la carga al punto del campo a medir. ### Un anillo cargado #### Sobre el eje del anillo 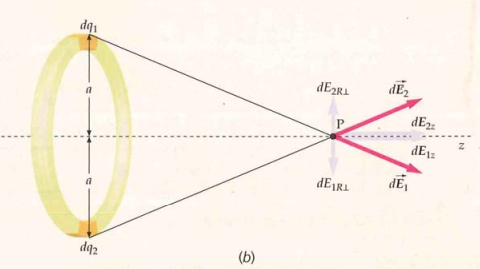![Pasted image 20231123120410.png](/img/user/Im%C3%A1genes/Pasted%20image%2020231123120410.png) - Radio del anillo: $a$ - Distancia de un punto del anillo al punto P: $r= \sqrt{x^2+a^2}$ - Los campos de las cargas diferenciales se anulan por pares en el eje perpendicular al eje del anillo - Por ende, el campo estará dirigido en la dirección paralela al eje del anillo - Toda la ecuación queda fuera de la integral, pues $x$ no cambia $$E_x = \frac{kQx}{(x^2+a^2)^{3/2}}\text{ [22.10]}$$ #### Varios anillos concéntricos cargados = Un disco cargado - En 22.10, se reemplaza $Q$ por $dq = 2\pi\sigma a\cdot da$ - Esto es la carga en un anillo de radio $a$ y anchura $da$ - Se integran todos los anillos del disco (variando $a$ en $[0; R], R=\text{Radio del disco}$) - Se hace cambio de variable con $u=x^2+a^2$

E_{x} = - 2 π k σ (1 - \frac{x}{\sqrt{1 + \frac{R^{2}}{x^{2}}}}), x > 0 [22.11]

\text{Si } x>>R \implies E_x = {kQ\over x^2}$$ (igual que ocurre con la carga lineal finita, muy lejos de esta, se comporta como una carga puntual) ### Un plano infinito cargado - El plano puede pensarse como un disco cargado de radio $R\to\infty$  - En las **proximidades del plano**, el campo $\vec E$ resulta: $$E_x = 2\pi k \sigma = {\sigma\over\epsilon_0},\space x>0 \text{ [22.13]}

Para valores negativos de $x$ , $E_{x}$ tendrá el valor negativo

Siguiente: Ley de Gauss >