Campo Eléctrico. Cálculo con ley de Gauss
Establecemos que:
- Si
- Es decir: si en un punto
de la superficie, la superficie es paralela al campo --o sea, que el vector normal es perpendicular al campo -- el campo será cero en ese punto:
- Es decir: si en un punto
Simetría plana
- Con un plano infinito, el cálculo es el mismo $$\vec E = {\sigma\over 2\epsilon_0}$$
Simetría esférica
Una carga puntual
- Para una carga puntual (la cual tiene simetría esférica) usamos una superficie gaussiana esférica de radio
, de modo que - O sea, el campo depende de la distancia de la superficie a la carga, y por la simetría este es constante en todos los puntos
- La superficie gaussiana tiene área
- El flujo neto es $$\phi_{neto} = \oint_S \vec E\cdot \hat n dA = \int_S E_r dA = E_r \oint dA \color{red} = E_r4\pi r^2$$
- Despejamos el campo $$E_r = {1\over 4\pi\epsilon_0}{q\over r^2} = {kq\over r^2} \text{ (ley de Coulomb)}$$
- ! Dedujimos la ley de Coulomb a partir de la ley de Gauss
(°ロ°) !
Una esfera conductora / una corteza esférica de carga
- & Tener una corteza esférica de carga es lo mismo que decir una esfera conductora
- Hay que recordar que un material conductor lleva la carga eléctrica en su superficie
- El campo dentro de la esfera hueca es
y hay una discontinuidad en el borde con la esfera:
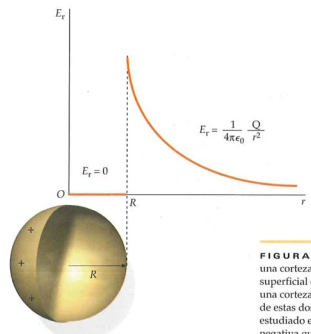
- Los campos
dentro de la esfera se cancelan mutuamente y tanto el campo eléctrico como el flujo dentro de la esfera es cero - Además de que
- Además de que
- Los campos
- Fuera de la esfera, el campo se puede contar como el de una carga puntual en el centro de la esfera
- Calcular con Fundamentos#Campo debido a una carga puntual
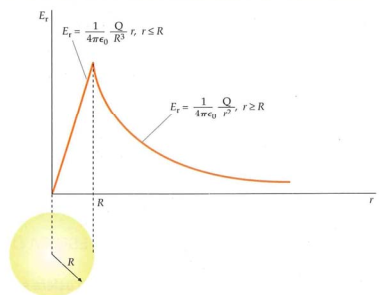
Una esfera de carga uniforme
- El campo
a una distancia del centro de una esfera de carga uniforme (de radio y densidad ) vine dado por:
- Esto se deriva relacionando --mediante la ley de Gauss-- el flujo que pasa por la superficie Gaussiana con el volumen de carga que encierra dicha superficie, que será una porción de la carga proporcional a la densidad
- En algún momento, se cancelan componentes entre los volúmenes de las dos esferas
- & Como la sup. Gaussiana siempre encierra una cantidad de carga, el campo es contínuo desde
Simetría cilíndrica
- Una distribución tiene simetría cilíndrica, si desde otra superficie cilíndrica que esté sobre el mismo eje que ella se puede apreciar el mismo campo constante
- El área de la superficie cilíndrica es
- El área de la superficie cilíndrica es
- La distribución de carga se comporta como una carga lineal (que suponemos infinita), y el campo no depende de la longitud de la carga encerrada, sólo su densidad