Cambio de variables

En integrales simples (repaso)

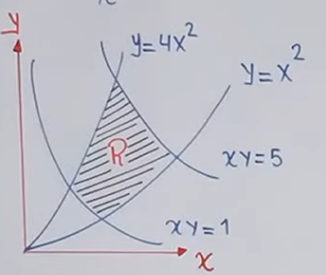
Pasted image 20230914114837.png

Si tenemos una región muy compleja, podemos cambiar los ejes de referencia para que los ejes sigan la forma $\int_{a}^{b} f (x) d x$
Si necesitamos cambiar $x$ a otra dada por una función $g (u)$ , debemos plantear el nuevo diferencial también, que será la derivada $g^{'} (u)$
Los límites también cambian para acomodar la región del nuevo espacio en el que se integra (la función $g$ se puede mover distinto que $x$ )

x = g (u); d x = g^{'} (u) ⟹ \int_{c}^{d} f [g (u)] g^{'} (u) d u

En integrales dobles

Si $f, g, h$ son derivables
Si $J (u, v) = 0$ sólo en puntos aislados
Entonces $\iint_{R} f (x, y) d x d y = \iint_{G} f [g (u, v), h (u, v)] \cdot | J (u, v) | d u d v$

Definición: Jacobiano

El determinante Jacobiano de la transformación de coordenadas $x = g (u, v), y = h (u, v)$ es $$J(u,v) = \begin{vmatrix}x_u & x_v \ y_u & y_v\end{vmatrix}=x_u\cdot y_v - y_u\cdot x_v$$
...donde $u, v$ son las variables a las que se cambia el sistema de ejes

Este mide cuánto cambia el área en torno de un punto de $G$ cuando $G$ se transforma en $R$ .
También se denota $J (u, v) = \frac{\partial (x, y)}{\partial (u, v)}$
^definicion-jacobiano