Clase

Regresión lineal por mínimos cuadrados

• Dado un conjunto de datos (puntos en el plano cartesiano), y una familia de funciones
• El objetivo es encontrar la función continua que se ajuste mejor a la tendencia general de los datos, según algún criterio
  • No necesariamente debe coincidir con todos los puntos
• ? Cómo elijo el criterio para elegir la familia de funciones?
  • ~ Generalmente, en Análisis Numérico vamos a trabajar con familias de rectas: $y=a_0+a_{1}x$
• Error residual o Discrepancia: Es la diferencia entre la altura de un dato y la recta de regresión
  • Simbolizado $e_i$ para el i-ésimo dato $(x_i,y_i)$
  • $e_i=y_i-y(x_i)=y_i-a_0-a_1{x}_i$
• Posibles criterios:
  1. Minimizar la suma de los errores residuales de todos los datos
     • $\sum _{i=1}^n{e}_i$
     • Esto es el error residual de un dato
     • El criterio es minimizar la suma de todos los errores residuales de todos los datos
     • ! Descartamos este criterio porque hay ciertos casos donde es ambiguo qué recta elegir
  2. Minimizar la suma de los valores absolutos de las discrepancias
     • O sea, minimizar $\sum _{i=1}^n|e_i|$
  3. MiniMax
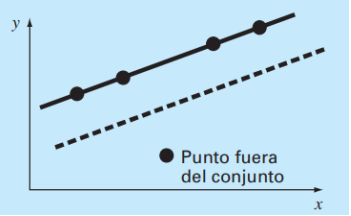
     • Minimizar la distancia máxima a la que un punto se encuentra de la línea
     • $max(|e_i|,i=1\dots n)$
     • ! Problema: Si tenemos 5 puntos: 4 alineados
  4. $ Mínimos cuadrados
     • Minimizar la suma de los cuadrados de los residuos
     • O sea, la expresión: $\sum _{i=1}^n(e_i{)}^2$
     • Es decir, encontrar los puntos mínimos de la expresión
       • Recordar de AM II: Encontrar los puntos críticos de una función de 2 variables $z=f(x,y)$
       • Al final de todo el desarrollo de los puntos críticos y un SEL, quedan dos fórmulas:
       • $ $$\begin{cases}\displaystyle a_1=\frac{n\sum[x_iy_i] - \sum x_i\sum y_i}{n\sum x_i^2 - (\sum x_i)^2} \ a_0 = \overline y - a_1 \overline x\end{cases}$$
       • Recordar que $\bar{x}=(\sum _{i=1}^n{x}_i)/n$
       • ~ La ventaja de este método es que consigue una única recta

Para graficar

• Tabulamos los datos con las siguientes columnas:

• Usando la última fila para guardar la sumatoria de las expresiones de cada columna
• Esto sirve para rápidamente hacer los cálculos auxiliares

Series de Fourier

• Polinomio de Taylor: Es un polinomio que aproxima una expresión no polinómica
  • Polinomio: Combinación lineal de $\{1,x,x^2,x^3,\dots \}$
• Serie de Fourier: Es una función o polinomio trigonométrico que aproxima una función periódica NO trigonométrica
  • $ Polinomio trigonométrico: Combinación lineal de $\{1,\cos (x),\cos (2x),\dots \}$
  • $ Función periódica (con periodo $T$): $f(t)=f(t+T)$
  • Siempre trabajamos con coseno
• Ejemplos de funciones periódicas no trigonométricas
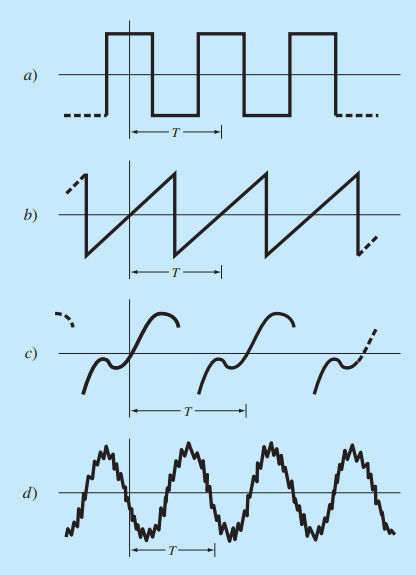
• $ Caso particular de la función periódica: $f(t)=A_0+C_1\cos ({\omega }_{0}t+\theta )$, donde
  • $A_0$: Valor medio
  • $C_1$: Amplitud
  • ${\omega }_0$: Frecuencia angular
  • $\theta$: Ángulo inicial
• Definimos
  • $A_1=C_1\cos \theta$
  • $B_1=-C_1\sin \theta$
  • De esta forma, $\theta =\arctan (-B_1/A_1)$

Ejercicios / Ejemplos

Hoja de práctica

![[]]

Preguntas