Clase

Métodos abiertos

En los métodos cerrados, la raíz se encuentra encerrada dentro de un intervalo, pero no sabemos a cuál de los extremos está más cerca. Además necesitan dos valores iniciales, al menos.

• En los métodos abiertos, se requiere como mínimo sólo un valor inicial
  • Puede tener varios valores iniciales, sólo que no necesariamente deben encerrar a la raíz
• Tienen la desventaja de que, estos métodos pueden divergir de la raíz

Método 1: Iteración simple de punto fijo

1. Se transforma la ecuación, despejando $x$: $f(x)=0\to x=g(x)$
2. Fórmula iterativa: $x_{i+1}=g(x_i)$
   • $x_0$ es un valor inicial cualquiera
3. ? Se busca la intersección entre las funciones $y=f(x)$ y $y=x$

• El error es $$\epsilon_a = |{x_{i+1}-x_i\over x_{i+1}}|\cdot 100%$$
• Sabemos que el método converge si el error verdadero disminuye según pasan las iteraciones
  • Esto se cumple si $|\frac{d}{dx}g(x)|<1$

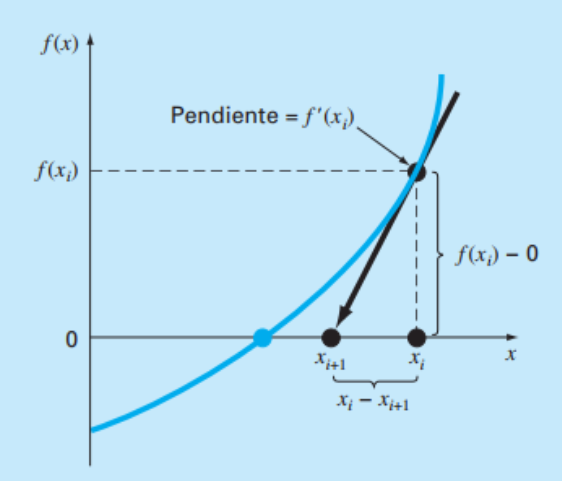
Método 2: Newton-Raphson

• Trabaja con la función original, y la pendiente de su derivada en el punto inicial $x_0$ (arbitrario)
  • $ Recordar ecuación punto-pendiente de una recta: $y-y_1=m(x-x_1)$
• Ecuación de la recta $t:y-f(x_0)=f^{\prime }(x_0)(x-x_0)$
• La aproximación en una iteración es la intersección entre $t$ y el eje x
  • 

1. Aproximación de la raíz: $x_{i+1}=x_i-\frac{f(x_0)}{f^{\prime }(x_i)}$

Método 3: Método de la secante

~

Ejercicios / Ejemplos

Hoja de práctica

~ Añadir foto de hoja

Preguntas